Virtual Reference Feedback Tuning is a data driven method used to design a controller for an unknown plant based on input/output measurements. The method uses a single set of input/output data generated by the plant without the need for specific experiments or model identification.

This is the first post in a series of posts detailing the method and explaining how to use it in MATLAB.

  1. Virtual Reference Feedback Tuning (this post)
  2. VRFT in MATLAB - Coming Soon

How Does It Work ?

The general idea behind VRFT is to transform the control problem of designing the controller into an identification problem. To use the VRFT method we need:

  • A reference Model. This is a model that describes the ideal behaviour of the closed loop system.
  • One set of input-output data on the plant. The input does not need to have any special characteristics.
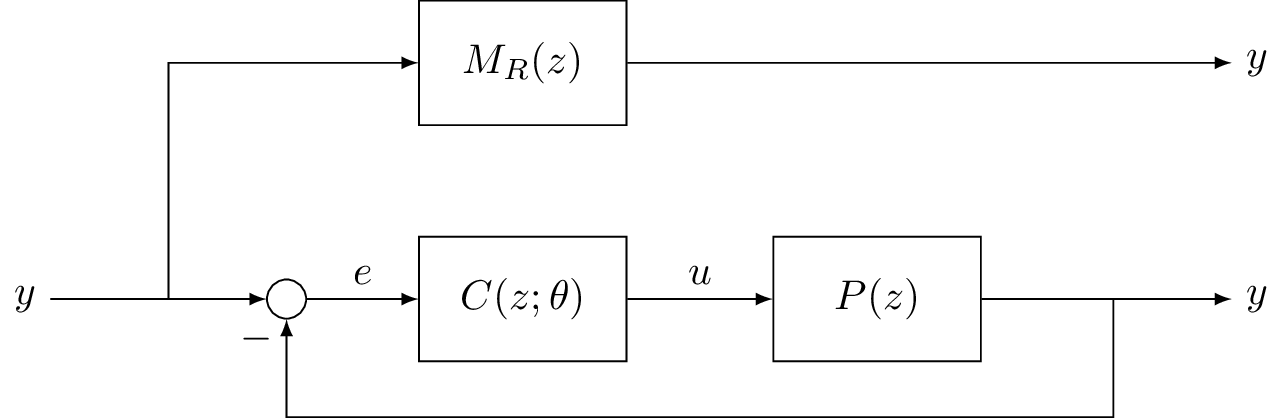
The block diagram of VRFT

Block diagram showing the closed loop control system and the reference model.

Note that the output of the reference model and the control loop are identical.

The output of the plant is the known from the I/O data that was previously collected. If we consider these measurements as the output of the reference model then we can build an input signal \(r(t)\) such that:

\begin{equation*} y(t) = M_R(z) r(t) \end{equation*}

This signal is the virtual reference. We want to make the closed loop behaviour of the system as close as possible to the reference model so we use this virtual reference as the set-point for the control loop. The output of the controller is the plant input \(u(t)\). This is the other known signal.

The input of the controller can easily be calculated:

\begin{equation*} e(t) = r(t) - y(t) \end{equation*}

Now that both the input and the output (\(u(t)\)) of the controller are known the control problem can be reduced to an identification problem.

A More Rigorous approach

It is assumed that the plant is a linear SISO discrete-time dynamical system described by a rational transfer function (\(P(z)\)).

We choose a reference model \(M_R(z)\) that describes the desired behaviour of the closed loop control system.

We determine a class of controllers \(C(z; \theta)\) that depend linearly on the parameter vector \(\theta\) such that:

\begin{equation*} C(z; \theta) = \beta(z)^T\theta^T \end{equation*}

Where:

  • \(\beta = [\beta_1(z), \beta_2(z), ..., \beta_n(z)]^T\) is a vector of linear transfer functions
  • \(\theta = [\theta_1, \theta_2, ... \theta_n]^T\) is the vector of parameters

The control objective is the minimisation of the following criterion:

\begin{equation*} \begin{aligned} J_{MR}(\theta) &= \left| \left( \frac{P(z)C(z; \theta)}{1 + P(z)C(z; \theta)} - M(z) \right) W(z) \right|_2^2 \\ &= \left| \left( T(z) - M(z) \right) W(z) \right|_2^2 \end{aligned} \end{equation*}

which is equivalent to minimising the difference between the closed loop system and the reference model scaled by an appropriate weighting function. The choice of this weighting function \(W(z)\) is up to the system designer and can be chosen to emphasize or de-emphasize performance in certain frequency bands.

An optimal choice of \(C(z; \theta)\) will produce a closed loop system whose transfer function is \(M(z)\). Thus, if the closed-loop system is fed a reference signal \(r(t)\) its output will be :

\begin{equation*} y(t) = T(z)r(t) = M(z)r(t) \end{equation*}

The VRFT method works by using the measured output (\(y(t)\)) to generate a reference signal \(\bar{r}(t)\) such that:

\begin{equation*} M(z)\bar{r}(t) = y(t) \end{equation*}

This is our so-called virtual reference, it does not exist in the physical world and is only used a tool to generate the optimal controller. The input of the controller is:

\begin{equation*} e(t) = \bar{r}(t) - y(t) \end{equation*}

The optimal controller must be such that when fed the virtual reference it produces the measured input (\(u(t)\)). Thus:

\begin{equation*} u(t) = C(z; \hat{\theta}) \bar{r}(t) \end{equation*}

Where \(\hat{\theta}\) is the optimal parameter vector.

To calculate the optimal parameter vector we can start by attempting to solve a slightly easier problem.

We apply a filter \(L(t)\) to the data. I will explain the reason for this filter and it's form soon but bear with me in the meantime.

\begin{equation*} e_L(t) = L(z)e(t) \quad, \quad y_L(t) = L(z)e(t) \end{equation*}

Now, consider the following performance index:

\begin{equation*} \begin{aligned} J^N_{VR}(\theta) &= \frac{1}{N} \sum_{t=1}^{N} \left( u_L(t) - C(z; \theta) \ e_L(t) \right)^2 \\ &= \frac{1}{N} \sum_{t=1}^{N}\left( u_L(t) - \beta^T(z)\theta \ e_L(t) \right)^2 \\ &= \frac{1}{N} \sum_{t=1}^{N}\left( u_L(t) - \varphi_L^T(t)\theta \right)^2, \quad \varphi_L = \beta^T(z) \ e_L(t) \end{aligned} \end{equation*}

Since this equation is quadratic in \(\theta\) the optimal value \(\hat{\theta}_N\) is an explicit function of the data:

\begin{equation*} \hat{\theta}_N = \left[ \sum_t \phi(t) \phi(t)^T \right]^{-1} \sum_t \phi(t)u(t) \end{equation*}

However, this doesn't seem to bring us any closer to solving our original problem of minimising \(J_{MR}\). This method though is useful because it is based purely on the data and is relatively easy to compute.

Before continuing we need to make a digression. Let's rewrite \(J_{MR}\) in the frequency domain:

\begin{equation*} \begin{aligned} J_{MR}(\theta) &= \frac{1}{2 \pi} \cdot \int_{-\pi}^{\pi} \left| \frac{PC(\theta)}{1 + PC(\theta)} - M \right|^2 \left| W \right|^2 d\omega \\ &= \frac{1}{2 \pi} \cdot \int_{-\pi}^{\pi} \left| \frac{PC(\theta)}{1 + PC(\theta)} - \frac{PC_0}{1 + PC_0} \right|^2 \left| W \right|^2 d\omega \\ &= \frac{1}{2 \pi} \cdot \int_{-\pi}^{\pi} \left| \frac{PC(\theta)[1 + PC_0] - PC_0[1 + PC(\theta)]}{[1 + PC(\theta)][1 + PC_0]} \right|^2 \left| W \right|^2 d\omega \\ &= \frac{1}{2 \pi} \cdot \int_{-\pi}^{\pi} \left| P \cdot \frac{C(\theta) - C_0}{[1 + PC(\theta)][1 + PC_0]} \right|^2 \left| W \right|^2 d\omega \\ \end{aligned} \end{equation*}

We can now go back to \(J_{VR}\).

If \(u(t)\) and \(y(t)\) can be considered realisations of stationary stochastic processes then as the amount of data grows (\(N \rightarrow \infty\)) the following holds:

\begin{equation*} J^N_{VR}(\theta) \rightarrow J_{VR}(\theta) \end{equation*}

And:

\begin{equation*} \begin{aligned} J_{VR}(\theta) &= E \left[ \left( u_L(t) - C(z; \theta)e_L(t) \right)^2 \right] \\ &= E \left[ L(z) \cdot \left( u(t) - C(z; \theta)e(t) \right)^2 \right] \end{aligned} \end{equation*}

We would like to get rid of \(e(t)\) in the equation to make it depend only on our initial data:

\begin{equation*} e(t) = \bar{r}(t) - y(t) = \bar{r}(t) - M_R(z)\bar{r}(t) = \left( 1 - M_R(z) \right) \cdot \bar{r}(t) \end{equation*}

And since:

\begin{equation*} r(t) = \frac{y(t)}{M_R} = \frac{P}{M_R} \cdot u(t) \end{equation*}

We can rewrite the criterion as:

\begin{equation*} \begin{aligned} J^N_{VR}(\theta) &= \frac{1}{N} \sum_{t=1}^{N} \left[u_L(t) - C(z; \theta) \cdot \left( 1 - M_R(z) \right) \cdot \frac{P}{M_R} \cdot u_L(t) \right]^2 \\ &= \frac{1}{N} \sum_{t=1}^{N} \left[ \left( L(z) \left( 1 - C(z; \theta) \cdot \frac{1 - M_R(z)}{M_R(z)} \cdot P \right) u_L(t)\right)^2 \right] \end{aligned} \end{equation*}

We also know that, by definition, \(M_R\) is:

\begin{equation*} M_R(z) = \frac{PC_0}{1 + PC_0} \quad \Rightarrow \quad 1 - M_R = \frac{1 + PC_0 - PC_0}{1 + PC_0} = \frac{1}{1 + PC_0} \end{equation*}

Which brings us to:

\begin{equation*} \begin{aligned} 1 - C(\theta) \cdot \frac{1 - M_R}{M_R} \cdot P &= \frac{1}{M_R} \left( M_R - PC(\theta) \left[ 1 - M_R \right] \right) \\ &= \frac{1}{M_R} \left( \frac{PC_0}{1 + PC_0} - \frac{PC(\theta)}{1 + PC_0} \right) \\ &= \frac{1}{M_R} \left( P \cdot \frac{C_0 - C(\theta)}{1 + PC_0} \right) \\ &= \frac{1}{M_R} P \cdot \left( C_0 - C(\theta) \right) \left( 1 - M_R \right) \end{aligned} \end{equation*}

By substituting this result back into \(J_{VR}\) we obtain:

\begin{equation*} J^N_{VR}(\theta) = E \left[ \left( \frac{L}{M_R} \cdot \left( C_0 - C(\theta) \right) \cdot \left( 1 - M_R \right) \right)^2 \right] \end{equation*}

The frequency-domain representation of this criterion is:

\begin{equation*} J_{VR}(\theta) = \frac{1}{2\pi} \int_{-\pi}^{\pi} \left| P \cdot \left( C_0 - C(\theta) \right) \left( 1 - M_R \right) \cdot \frac{L}{M_R} \right|^2 \Phi_u \ d\omega \end{equation*}

Where, \(\Phi_u\) is the power density of \(u(t)\).

If \(C_0(z) \in C(z; \theta)\) and \(J_{VR}(\theta)\) has a unique minimum then minimizing \(J_{VR}(\theta)\) will always yield \({C_0(z)}\) independently of the value of \(L(z)\).

Notice the similarity between the expressions of \(J_{MR}\) and \(J_{VR}\). With a proper choice of the pre-filter \(L(z)\) we can make them equal.

If:

\begin{equation*} \left| L \right|^2 = \left| \frac{M_R W}{1 + PC(\theta)} \right|^2 \cdot \frac{1}{\Phi_u} \end{equation*}

Then,

\begin{equation*} \begin{aligned} J_{VR}(\theta) &= \frac{1}{2\pi} \int_{-\pi}^{\pi} \left| P \cdot \frac{C_0 - C(\theta)}{1 + PC_0} \cdot \frac{W}{1 + PC(\theta)} \right|^2 \ d\omega \\ &= \frac{1}{2 \pi} \int_{-\pi}^{\pi} \left| P \cdot \frac{C(\theta) - C_0}{[1 + PC(\theta)][1 + PC_0]} \right|^2 \left| W \right|^2 \ d\omega = J_{MR}(\theta) \end{aligned} \end{equation*}

Unfortunately this pre-filter is not practical since it depends on knowing the plant model \(P\). However, if \(C(z; \theta)\) is a good approximation of \(C_0(z)\) then:

\begin{equation*} \left( 1 - M_R \right) = \frac{1}{1 + PC(z; \theta)} \approx \frac{1}{1 + PC_0(z)} \end{equation*}

Thus, \(L(z)\) can be written as:

\begin{equation*} L(z) = \left| \left(1 - M_R \right) \cdot M_R \cdot W \right|^2 \cdot \frac{1}{\Phi_u} \end{equation*}

This formulation of the pre-filter is completely known. This proves that \(J_{MR}\) and \(J_{VR}\) are equivalent and that by solving the simpler problem (\(J_{VR}\)) we also solve the original problem (\(J_{MR}\)).

Recap

In conclusion, the VRFT method can be broken down into a set of relatively simple steps:

  • Choose a reference model \(M_R\) and class of controllers \(C(z; \theta)\)
  • Calculate the pre-filter \(L(z)\)
  • Compute the optimal parameter vector \(\hat{\theta}_N\)

The VRFT method can be extended to cases where the signal is noisy, we will discuss this in a later post. The VRFT method has also been extended to cascade control systems. This too will be the subject of a later post.